Was sind elliptische Kurven?
In diesem Video gehen wir der Frage nach, was sind eigentlich elliptische Kurven? Aus der Sichtweise der Mathematik ist eine elliptische Kurve durch die sogenannte Weierstrassgleichung beschrieben.
- Was ist Kryptographie?
- Vertraulichkeit, Integrität und Authentizität.
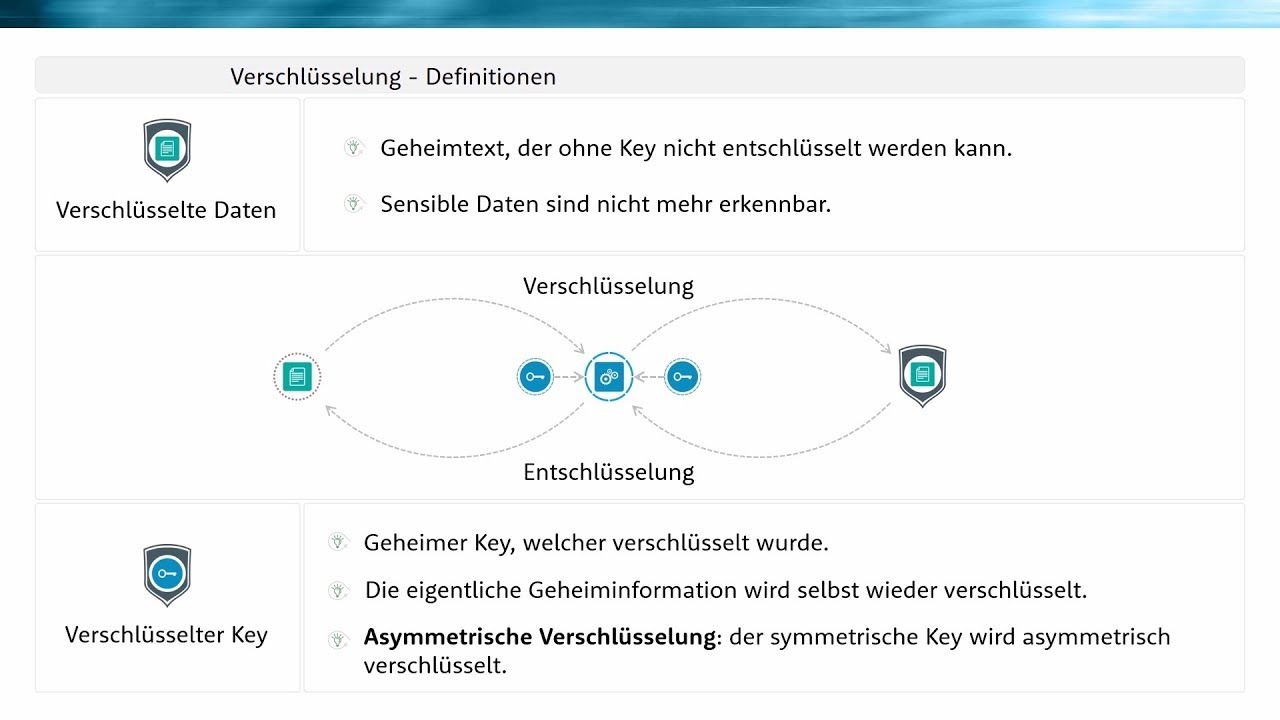
- Daten und verschlüsselte Daten.
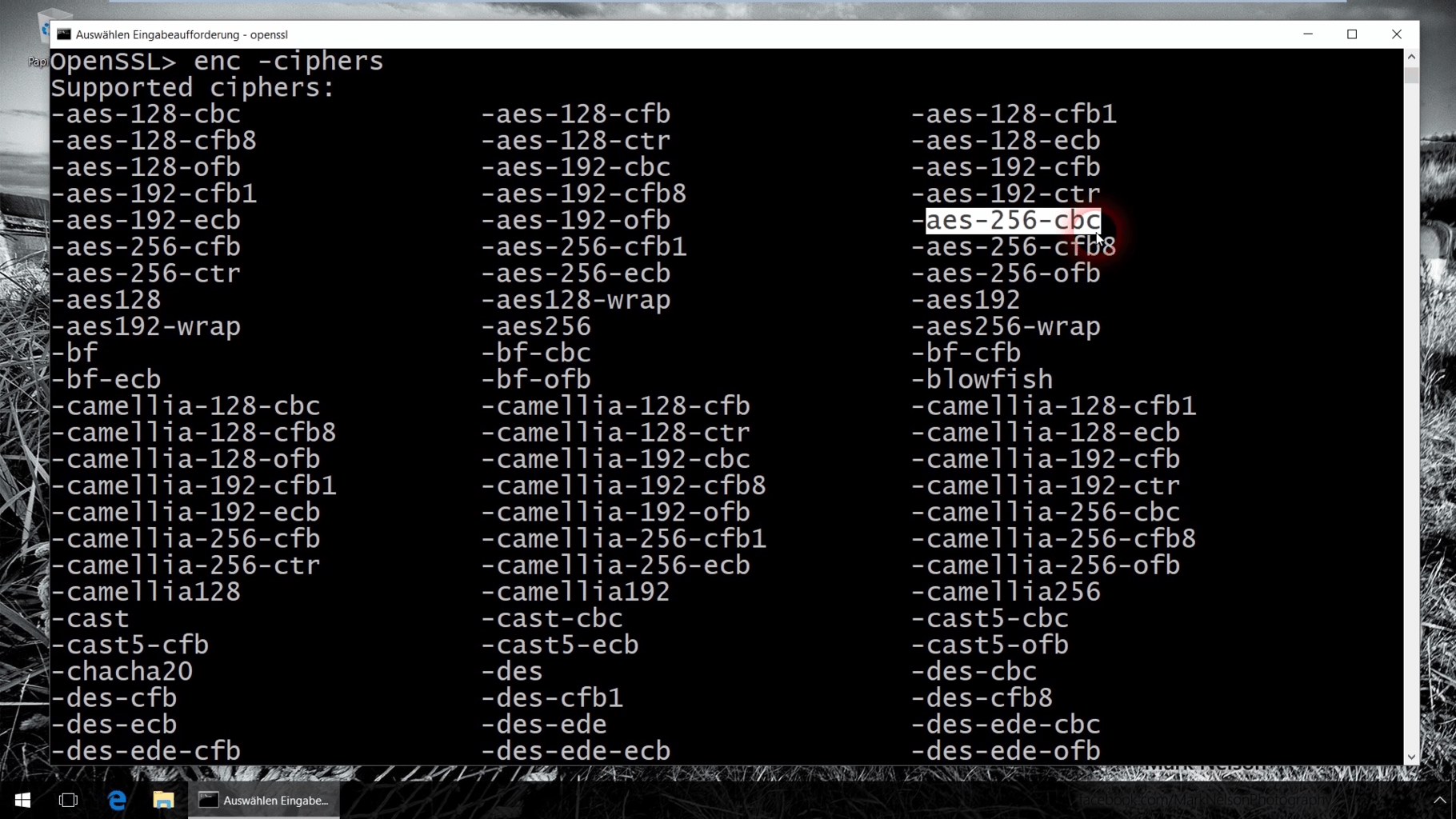
- Algorithmen und verschlüsselte Keys.
Auszug aus dem Video
Aus der Sichtweise der Mathematik ist eine elliptische Kurve durch die sogenannte Weierstrassgleichung beschrieben, deren Formel lautet:
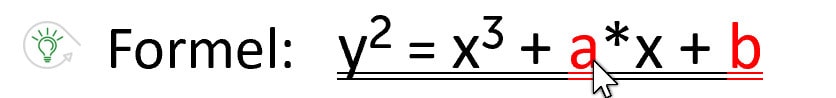
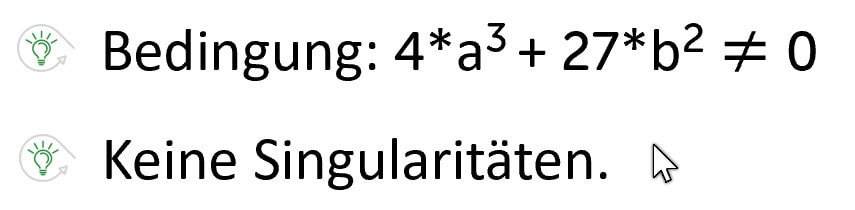
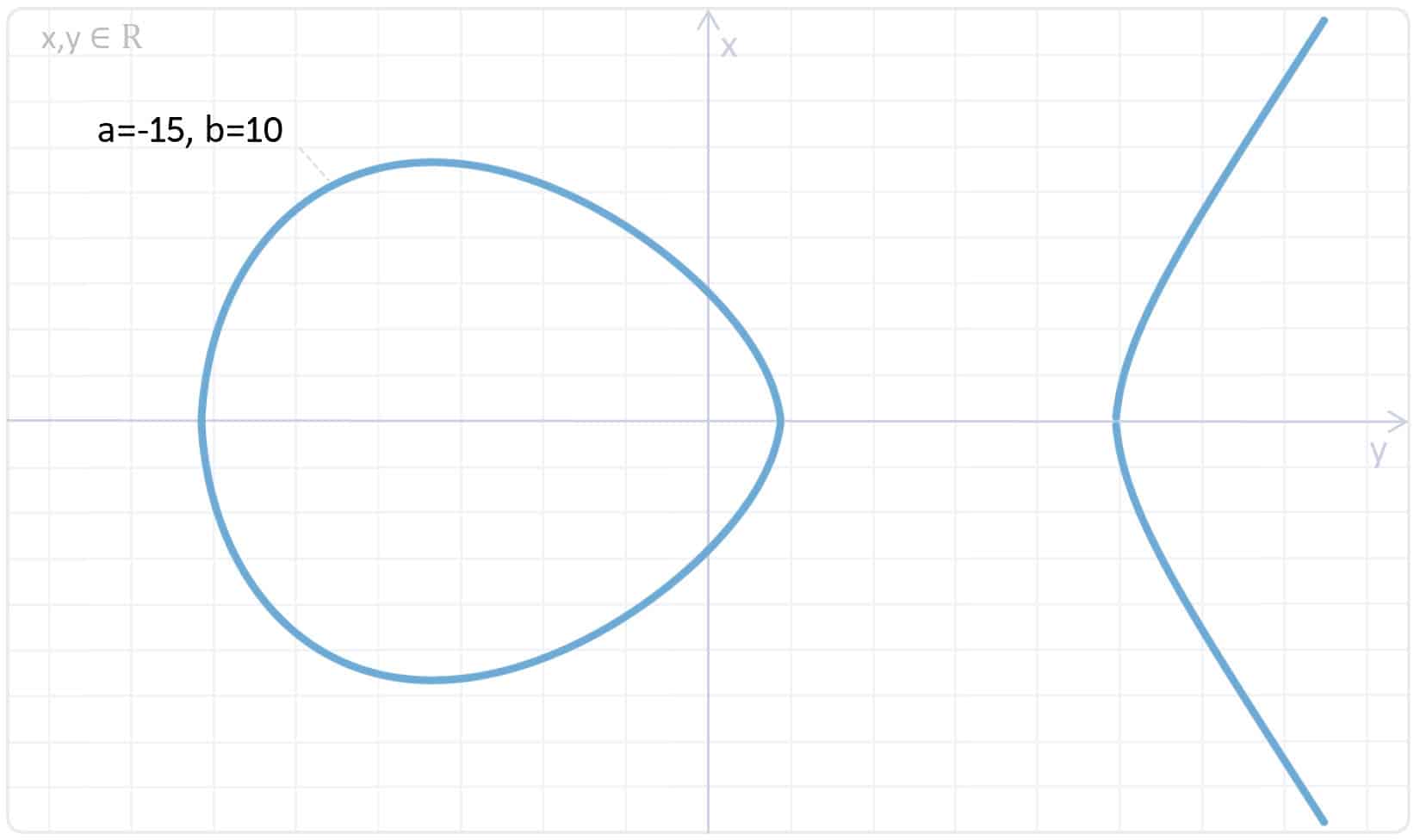
Es handelt sich hierbei also um eine glatte algebraische Kurve der 3. Ordnung. Der Wert für y kann durch die Koeffizienten a und b beeinflusst werden. Wenn Ihr die elliptische Kurve mit den Koeffizienten a = -15 und b = 10 grafisch darstellt, dann sieht die Form der Kurve aus, wie eine Insel mit Küste. Die Werte für a und b sind fast frei wählbar, die Koeffizienten müssen dabei aber hier diese Bedingung erfüllen. Diese Bedingung sorgt dafür, dass keine Singularitäten entstehen.
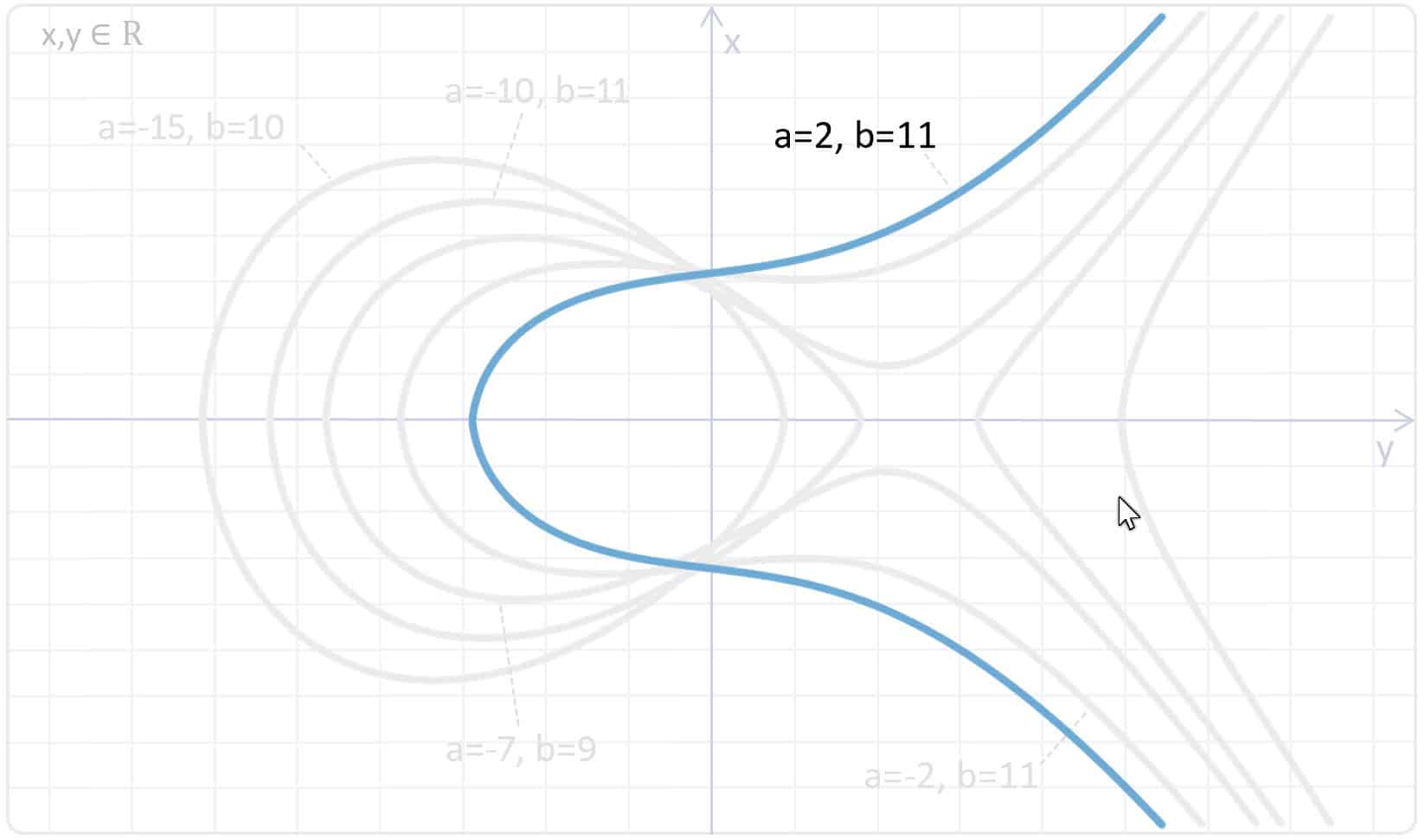
Das Prinzip der elliptischen Kurve wurde um 1985 von Neal Koblitz und Victor Miller unabhängig voneinander erfunden. In der Kryptographie werden die elliptischen Kurven mit dem Diffie Hellman Algorithmus oder dem DSA kombiniert. Vor den Bezeichnern DH und DSA wird bei Anwendung dann einfach das Kürzel EC davorgesetzt. Wenn Ihr zum Beispiel die Website von Udemy.com aufruft und euch die Informationen über die TLS-Verbindung vom Browser anzeigen lasst, dann seht Ihr, das derzeit das ECDHE verwendet wird, um eben eure Kommunikation mit Udemy zu verschlüsseln.
Eigenschaften einer elliptischen Kurve
Wenn wir jetzt eine Gerade durch die Kurve ziehen, so wie hier dargestellt, dann entstehen 3 Schnittpunkte. Durch die Form des Kleiderbügels kann es auch sein, dass eine Gerade die elliptische Kurve an den Wendepunkten lediglich berührt, aber nicht schneidet. Dieser Berührpunkt zählt dann quasi doppelt, sodass auch hier wieder 3 Schnittpunkte entstehen.
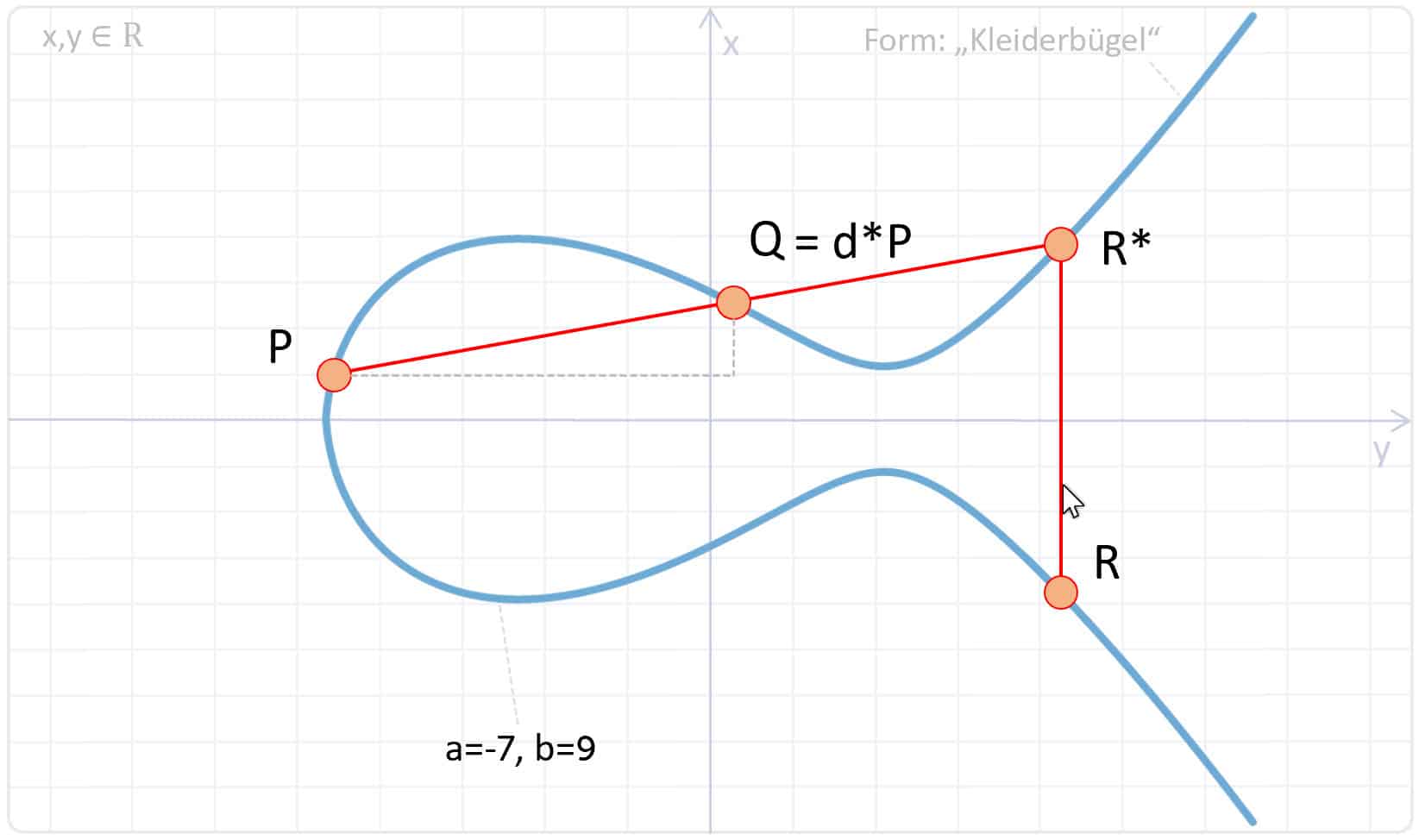

Die Schnittpunkte nenne ich jetzt mal P, Q und R. Alle drei Punkte besitzen jeweils eine x und y Koordinate. Wir werden später noch sehen, dass 3 Schnittpunkte auf einer Geraden für die Kryptographie mit elliptischen Kurven sehr wichtig sind, weshalb wir uns jetzt mal die Eigenschaften der Schnittpunkte ansehen werden. Wenn wir zum Beispiel die Punkte P und Q addieren, dann entsteht als Ergebnis wieder ein Punkt auf der elliptischen Kurve und ich nenne diesen mal R. Spiegelt man diesen Punkt auf der Kurve, so errechnet sich genau der Punkt R*. Das bedeutet, die drei Punkte P, Q und R auf der Geraden haben also eine Beziehung zueinander. Werden P und Q addiert, dann bildet der Punkt R* den Spiegelpunkt zum Ergebnis der Addition.
Auf diese 3 Punkte lassen sich einige mathematische Regeln anwenden. Zum Beispiel können die Punkte P und Q vertauscht werden, ohne das sich das Ergebnis der Addition verändert. Beide Punkte sind also kommutativ zueinander. Ebenso lässt sich das Assoziativgesetzt und das Distributivgesetzt auf die Punkte anwenden.
Interessant ist die skalare Multiplikation von Q = P * d, weil diese entscheidend ist für die Kryptographie. Wenn der Punkt P mit einem bestimmten Skalar „d“ multipliziert wird, dann errechnet sich der Punkt Q. Wir werden später noch sehen, das der Punkt Q, also das Ergebnis der Multiplikation zum public Key gehört, während das Skalar selbst den private Key darstellt. In der Grafik kann also der Punkt Q durch P*d ersetzt werden. Die Bedingungen bleiben aber gleich: das Skalar d (also der private Key) muss einen entsprechenden Wert aufweisen, sodass eine Multiplikation mit P wieder ein Punkt auf der elliptischen Kurve bildet, hier als Q bezeichnet. Deren Addition mit P (also P+Q) errechnet dann den Punkt R, der ebenfalls auf der elliptischen Kurve zu finden sein muss. Das Skalar d als private Key muss also alle diese Bedingungen hier erfüllen, deshalb habe ich euch das hier mal grafisch dargestellt.
Elliptische Kurven und endliche Körper
Ok, bisher hab ich die elliptische Kurve als durchgezogene Linie dargestellt, was bedeutet, das x und y Teil der reellen Zahlen sind. Das Problem ist, dass reelle Zahlen für die Kryptographie ungeeignet sind, weil deren Berechnungen viel zu langsam wäre und es können Rundungsfehler auftreten.
Deshalb wird in der Kryptographie immer nur mit ganzen Zahlen gearbeitet. Das bedeutet, wir müssen als nächstes eine Gruppe von Zahlen über eine elliptische Kurve definieren und dazu verwenden wir den Modulo mit einer Primzahl p. Modulo bedeutet hier, dass wir auf beiden Seiten der Formel, das Ergebnis mit einer Primzahl dividieren und der Rest der Division wird dann als Wert verwendet. Als Ergebnis können dann nur noch ganze Zahlen innerhalb des Zahlenbereichs zwischen 0 und der Primzahl entstehen, was die Menge der Ergebnisse automatisch begrenzt. In der Kryptographie wird daher eine sehr große Primzahl gewählt, sodass genügend Punkte auf der Kurve zur Verfügung stehen und damit auch ausreichend viele Zahlen in der Gruppe. Durch die Modulooperation in der elliptischen Kurve entsteht dann als Ergebnis eine Punktwolke.
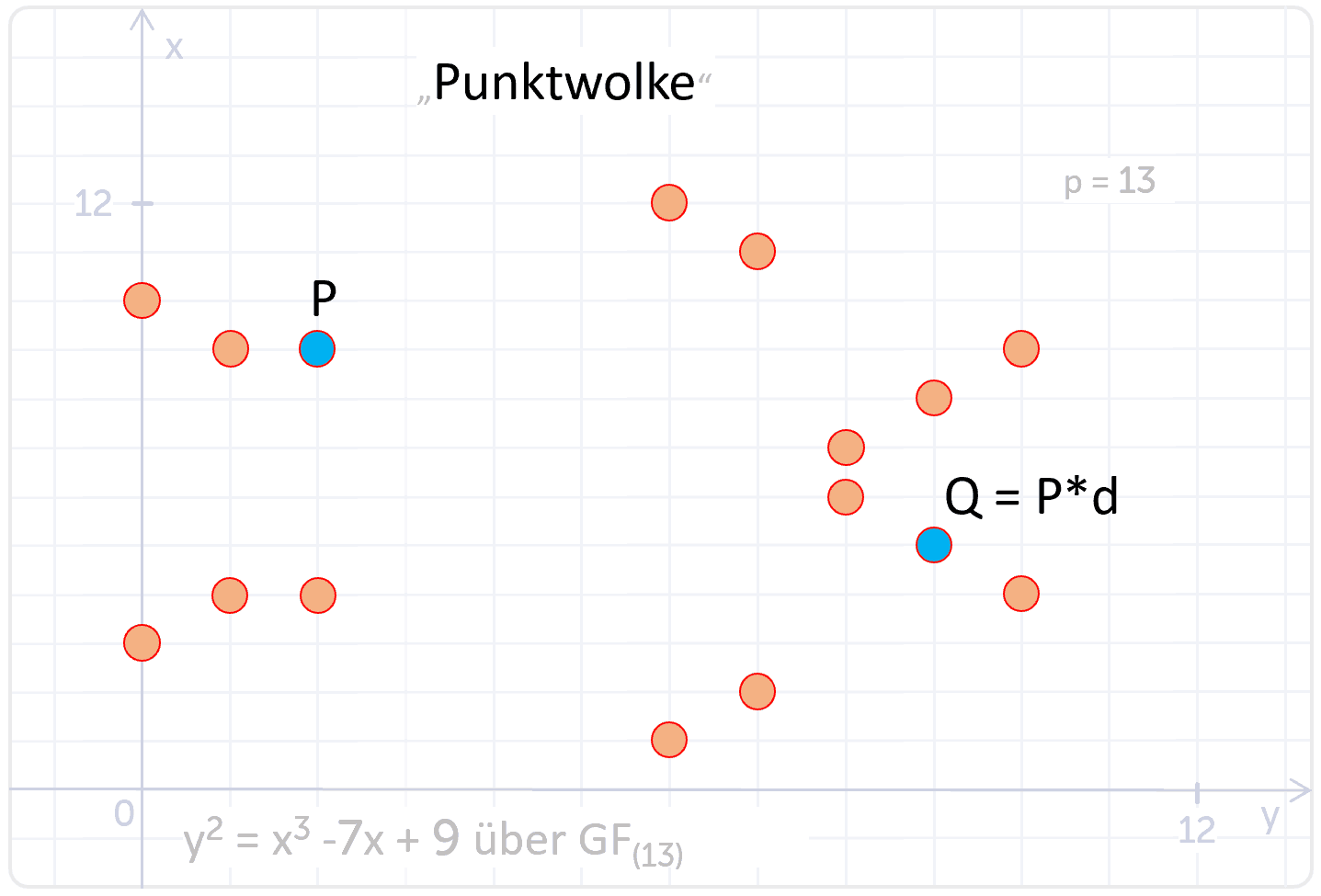

Bedingung ist allerdings, dass die mathematischen Regeln nach wie vor ihre Gültigkeit behalten. Das heißt die Punkte innerhalb der Punktwolke sollten natürlich auch kommutativ, assoziativ und Distributiv sein, ebenso sollte die Multiplikation mit einem Skalar funktionieren. Die endliche Gruppe besitzt dieselben Operationen, unterscheidet sich aber dadurch, dass die Anzahl der Elemente auf eine bestimmte Menge begrenzt ist. Die Multiplikation eines Punktes aus der Punktwolke mit einem Skalar muss wieder einen Punkt innerhalb der Punktwolke ergeben. Das ist wichtig für die Kryptographie. Der private Key ist letztlich nur ein skalarer Wert, wie zum Beispiel „d“. Zum public Key gehört ein Punkt innerhalb der Punktwolke zum Beispiel P. Und die Multiplikation mit dem skalaren Wert, also P mal d, muss dann wieder ein Punkt innerhalb der Wolke sein, wie zum Beispiel der Punkt Q.
Weitere Videos in diesem Onlinekurs:
Jetzt zum Newsletter anmelden und als Dankeschön einen exklusiven Gutschein Code für unsere Kryptographie Kurse erhalten.
Bleibe informiert zum Thema Kryptographie, erhalte neue Kurse als einer der Ersten und nimm an exklusiven Rabattaktionen teil. Wir verschicken keinen Spam und du kannst den Newsletter jederzeit wieder abbestellen.